Yhyjyk

Esta página ou secção cita fontes confiáveis e independentes, mas que não cobrem todo o conteúdo, o que compromete a verificabilidade (desde fevereiro de 2017). Por favor, insira mais referências no texto. Material sem fontes poderá ser removido. —Encontre fontes: Google (notícias, livros e acadêmico)

O ciclo de Otto é um ciclo termodinâmico idealizado que descreve o funcionamento de um típico motor de pistão de ignição com faísca^[1]. É o ciclo termodinâmico mais comum em motores de automóveis.

O ciclo de Otto é uma descrição do que acontece com uma massa de gás submetida a trocas de calor e variações de pressão, temperatura e volume. A massa de gás sujeita a essas mudanças é chamada de sistema, logo o sistema, neste caso, é definido como o fluido (gás) dentro do cilindro. Ao descrever as mudanças que ocorrem dentro do sistema, também descreverá em inverso, o efeito do sistema sobre o meio ambiente. No caso do ciclo Otto, o efeito será produzir o trabalho líquido suficiente para impulsionar um automóvel e seus ocupantes.

O ciclo Otto no diagrama pressão x volume é construído a partir de:

Parte superior e inferior do ciclo: um par de processos quase paralelos e isentrópicos (sem atrito e adiabática reversível).

Lados esquerdo e direito do ciclo: um par de processos isocóricos paralelos (volume constante).

O processo isentrópico de compressão ou expansão implica que não haverá ineficiência (perda de energia mecânica) e não haverá transferência de calor para dentro ou para fora do sistema durante esse processo. Portanto, o cilindro e o pistão são assumidos adiabáticos durante esse tempo. O trabalho é realizado no sistema durante o processo de compressão isentrópica inferior. O calor flui no ciclo Otto através do processo de pressurização esquerdo e parte dele flui para trás através do processo de despressurização direto. O somatório do trabalho adicionado ao sistema mais o calor adicionado menos o calor removido produz o trabalho mecânico líquido gerado pelo sistema.

Os processos são descritos por^[2]

• Processo 0-1 uma massa de ar entra no conjunto pistão / cilindro a pressão constante.


• O processo 1-2 é uma compressão adiabática (isentrópica) da carga à medida que o pistão se move do ponto morto inferior (PMI) para o ponto morto superior (PMS).


• Processo 2-3 é uma transferência de calor de volume constante para o gás de trabalho de uma fonte externa enquanto o pistão está no ponto morto superior. Este processo destina-se a representar a ignição da mistura combustível-ar e a subsequente queima rápida.


• Processo 3-4 é uma expansão adiabática (isentrópica).


• O processo 4-1 completa o ciclo por um processo de volume constante em que o calor é rejeitado do ar enquanto o pistão está no ponto morto inferior.


• Processo 1-0, a massa de ar é liberada para a atmosfera em um processo de pressão constante.

O ciclo Otto consiste em compressão isentrópica, adição de calor em volume constante, expansão isentrópica e rejeição de calor em volume constante. No caso de um ciclo Otto de quatro tempos, tecnicamente, existem dois processos adicionais: um para o escape de calor residual e produtos de combustão a pressão constante (isobárica) e outro para a ingestão de ar fresco rico em oxigênio também a pressão constante ; No entanto, estes são muitas vezes omitidos em uma análise simplificada. Mesmo que esses dois processos sejam críticos para o funcionamento de um motor real, em que os detalhes da transferência de calor e química de combustão são relevantes, para a análise simplificada do ciclo termodinâmico, é mais conveniente assumir que todo o calor residual é Removido durante uma única mudança de volume.

História |

O motor de quatro-tempos foi primeiramente patenteado por Alphonse Beau de Rochas em 1861. ^[3] E antes, em aproximadamente 1854 – 57, foi espalhado boatos de que dois italianos (Eugenio Barsanti e Felice Matteucci) teriam inventado um motor muito semelhante, mas a patente foi perdida.

A primeira pessoa a construir um motor de quatro tempos foi o engenheiro alemão Nikolaus Otto^[4] .  Um motor estacionário que utiliza uma mistura gás de carvão como combustível . Este princípio de quatro tempos hoje é comumente conhecido como o ciclo de Otto e motores de quatro tempos usando velas de ignição muitas vezes são chamadas motores Otto.

O processo |

Diagrama Pressão X Volume

O sistema é definido como a massa de ar que é extraída da atmosfera para dentro do cilindro, comprimida pelo pistão e aquecida pela faísca de ignição injetada pelo combustível, permitindo expandir a medida que comprime o pistão, e finalmente exaurir o ar de volta para a atmosfera. A massa de ar segue com seu volume, pressão e variação de temperatura durante as várias etapas termodinâmicas. O pistão é capaz de se mover ao longo do cilindro, o volume de ar muda de acordo com a posição do pistão no cilindro. Os processos de compressão e expansão do gás, induzido pelo pistão é ideal e reversível, isto é, nenhum trabalho útil é perdido pela turbulência ou pelo atrito, e nenhum calor é transferido de ou para o gás durante esses dois processos. A energia é adicionada ao ar, pela combustão do combustível. O trabalho útil é extraído pela expansão do gás no cilindro. Depois de completa a expansão no cilindro, o calor remanescente é extraído, e finalmente o gás é liberado para o meio ambiente. O trabalho mecânico útil é produzido durante a expansão do processo, e parte dele é usado para comprimir a massa de ar do ciclo seguinte. O trabalho útil mecânico produzido, menos o usado para o processo de compressão é o trabalho liquido obtido, que pode ser usado para propulsão ou para dirigir outras máquinas. Alternativamente o trabalho útil obtido é a diferença entre o calor adicionado e o calor removido

Diagrama Temperatura-Entropia
O diagrama idealizado de quatro estágios do ciclo de Otto:
o estágio de admissão (0-1) é realizado por um processo isobárico de expansão, seguido por processo adiabático de  compressão . Através da combustão do combustível, calor é adicionado em um processo isocórico, seguido por um processo adiabático de expansão, caracterizando o ciclo de  força . O ciclo é fechado pela  exaustão , caracterizada por processo de refrigeração isocórica e compressão isobárica.

O ciclo ideal de Otto pode ser representado pelas seguintes etapas:

1. Admissão isobárica 0-1.


2. Compressão adiabática 1-2.


3. Combustão isocórica 2-3, expansão adiabática 3-4.


4. Abertura de válvula 4-5, exaustão isobárica 5-0.

A taxa de compressão volumétrica é definida por: α=V2V1displaystyle alpha =frac V_2V_1.

Onde:

0<α<1displaystyle 0<alpha <1 pois V2displaystyle V_2 é sempre maior que V1displaystyle V_1

V2displaystyle V_2 é o volume final após a compressão na etapa 1-2

V1displaystyle V_1é o volume inicial antes da compressão na etapa 1-2

O rendimento térmico teórico de um motor térmico pode ser pensado como a quantidade de calor transmitida pela fonte quente que é necessário para realizar um determinado trabalho sendo que a fonte fria é um subproduto não aproveitado.

Temos então:

W=Δ.Qdisplaystyle W=Delta .Q - Equação (1) Primeira Lei da Termodinâmica

μ=WQ1displaystyle mu =frac WQ_1 - Equacão (2) Onde Q1displaystyle Q_1 é a quantidade de calor da fonte quente e Wdisplaystyle W o trabalho realizado pelo motor

Realizando a substituição da eq.1 em 2, tem-se:

μ=Q1−Q2Q1=1−Q2Q1displaystyle mu =frac Q_1-Q_2Q_1=1-frac Q_2Q_1 - Equação (3) - Eficiência Teórica de um motor térmico

Onde:

Q1displaystyle Q_1 é o calor cedido ao sistema para a realização do trabalho

Q2displaystyle Q_2 é o calor perdido pelo sistema na realização do trabalho

Para cada ciclo térmico, temos que o calor cedido e perdido pelo sistema vai depender de qual é o processo térmico realizado. No ciclo de Otto, seguindo o diagrama Temperatura-Entropia (segunda figura ao lado direito), o calor entra na etapa 2-3 (transformação isocórica) e sai na etapa 4-1 também isocórica.

Por momento, a eficiência do Ciclo de Otto é dada por:

μ=1−1αγ−1displaystyle mu =1-frac 1alpha ^gamma -1. Equação (4)

Onde γdisplaystyle gamma é o Coeficiente de expansão adiabática.

Ciclos reais |

Ciclo a quatro tempos

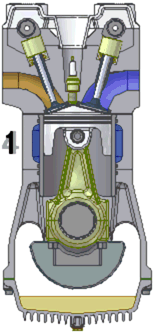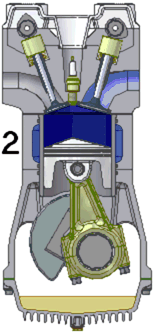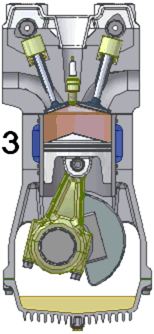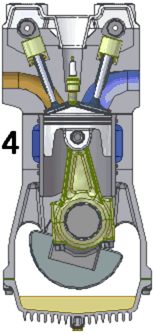
Os ciclos termodinâmicos associados às máquinas reais se diferem sensivelmente da idealização, já que os processos ocorrem apenas de forma aproximada à maneira descrita e que os motores estão suscetíveis a fenômenos não reversíveis como o atrito.

Ciclo mecânico |

Se limitando para os motores a combustão interna de duas válvulas, nas quais, são ligadas ao comando de válvula. Uma delas tem a função é classificada como válvula de admissão (à direita na animação), que permite a introdução no cilindro de uma mistura gasosa composta por ar e combustível e outra classificada como válvula de escape (à esquerda na animação), que permite a expulsão para a atmosfera dos gases queimados, o ciclo de funcionamento de um motor de combustão a 4 tempos é o seguinte:

1. Com o êmbolo (também designado por pistão) no PMS (ponto morto superior) é aberta a válvula de admissão, enquanto se mantém fechada a válvula de escape. A dosagem da mistura gasosa é regulada pelo sistema de alimentação, que pode ser um carburador ou pela injeção eletrônica, em que se substitui o comando mecânico destes sistemas por um eletrônico e conseguindo-se assim melhores prestações, principalmente quando solicitadas respostas rápidas do motor. O pistão é interligado a biela e esta por sua vez é interligada ao eixo de manivelas (virabrequim) impulsionado-o em um movimento de rotação. O pistão move-se então até ao PMI (ponto morto inferior). A este passeio do êmbolo é chamado o primeiro tempo do ciclo, ou tempo de admissão.


2. Fecha-se nesta altura a válvula de admissão, ficando o cilindro cheio com a mistura gasosa, que é agora comprimida pelo pistão, impulsionado no seu sentido ascendente em direcção à cabeça do motor por meio de manivelas até atingir de novo o PMS. Na animação observa-se que durante este movimento as duas válvulas se encontram fechadas. A este segundo passeio do êmbolo é chamado o segundo tempo do ciclo, ou tempo de compressão.


3. Quando o êmbolo atingiu o PMS, a mistura gasosa que se encontra comprimida no espaço existente entre a face superior do êmbolo e a cabeça do motor, denominado câmara de combustão, é inflamada devido a uma faísca produzida pela vela e "explode". O aumento de pressão devido ao movimento de expansão destes gases empurra o êmbolo até ao PMI, impulsionando desta maneira por meio de manivelas e produzindo a força rotativa necessária ao movimento do eixo do motor que será posteriormente transmitido às rodas motrizes. A este terceiro passeio do êmbolo é chamado o terceiro tempo do ciclo, tempo de explosão, tempo motor ou tempo útil, uma vez que é o único que efectivamente produz trabalho, pois durante os outros tempos, apenas se usa a energia de rotação acumulada no volante ("inércia do movimento"), o que faz com que ele ao rodar permita a continuidade do movimento por meio de manivelas durante os outros três tempos.


4. O cilindro encontra-se agora cheio de gases queimados. É nesta altura, em que o êmbolo impulsionado por meio de manivelas retoma o seu movimento ascendente, que a válvula de escape se abre, permitindo a expulsão para a atmosfera dos gases impelidos pelo êmbolo no seu movimento até ao PMS, altura em que se fecha a válvula de escape. A este quarto passeio do êmbolo é chamado o quarto tempo do ciclo, ou tempo de exaustão(escape).

• Após a expulsão dos gases o motor fica nas condições iniciais permitindo que o ciclo se repita.

Análise de Ciclo |

Nas etapas 1-2 e 3-4 (diagrama TxS) é realizado trabalho mas como processo é adiabático, não ocorre transferência de calor. Durante as etapas 2-3 e 4-1 os processos térmicos são isocóricos, ou seja, a transferência de calor ocorre mas nenhum trabalho é efetuado. O trabalho é realizado durante um processo térmico isocórico é zero porque para ocorrer o trabalho necessita que se tenha uma variação no volume. Partindo da equação do rendimento térmico conforme o demostrado acima:

μ=1−Q2Q1displaystyle mu =1-frac Q_2Q_1 - Equação (5)

Temos que Q1displaystyle Q_1 e Q2displaystyle Q_2 são dados por:

Q1=cv(T3−T2)displaystyle Q_1=c_v(T_3-T_2)

Q2=cv(T4−T1)displaystyle Q_2=c_v(T_4-T_1)

Onde:

Cvdisplaystyle C_v é o calor específico molar a volume constante

No ciclo de Otto, não há transferência de calor durante os processo térmicos das etapas 1-2 e 3-4 porque são processos adiabáticos reversíveis. Sendo assim, temos que o calor cedido e perdido pelo sistema ocorrem respectivamente nas etapas 2-3 e 4-1.^[5]

Inserindo a equação específica de calor na equação de eficiência térmica, temos:

η=1−(cv(T4−T1)cv(T3−T2))displaystyle eta =1-left(frac mathit c_v(mathit T_4-mathit T_1)mathit c_v(mathit T_3-mathit T_2)right) - Equação (6)

Através de rearranjo:

η=1−(T1T2)(T4/T1−1T3/T2−1)displaystyle eta =1-left(frac mathit T_1mathit T_2right)left(frac mathit T_4/mathit T_1-1mathit T_3/mathit T_2-1right) - Equação (7)

A seguir, analisando os diagramas T4/T1=T3/T2displaystyle T_4/T_1=T_3/T_2, assim ambos podem ser omitidos. A equação se reduz para:

Equação 2:

η=1−(T1T2)displaystyle eta =1-left(frac mathit T_1mathit T_2right) - Equação (8)

Visto que o ciclo de Otto é um processo isentrópico as equações isentrópicas de gases ideais e relações pressão/volume constantes podemos usar a relação abaixo:

(T2T1)=(V1V2)(γ−1)=r(γ−1)displaystyle left(frac T_2T_1right)=left(frac V_1V_2right)^(gamma -1)=r^(gamma -1)

Onde:

γ=(cpcv)displaystyle gamma =left(frac mathit c_pc_vright) - Coefiente de expansão adiabátiaca

r=(V1V2)displaystyle r=left(frac mathit V_1mathit V_2right) - Taxa de compressão

Aplicando estas relações na Equação 8, temos que a eficiência térmica final pode ser expressa como:^[5]

η=1−(1r(γ−1))displaystyle eta =1-left(frac 1r^(gamma -1)right) - Equação (9)

Da análise da equação 6 é evidente que a eficiência do ciclo de Otto depende diretamente da taxa de compressão rdisplaystyle mathit r. Desde que γdisplaystyle gamma para o ar é 1.4, um aumento em rdisplaystyle mathit r irá produzir um aumento em ηdisplaystyle eta . Entretanto, o γdisplaystyle gamma para produtos da combustão da mistura combustível/ar é normalmente assumida como 1.3 aproximadamente.
A argumentação acima implica que é mais eficiente ter uma taxa de compressão alta. O padrão de compressão é aproximadamente 10:1 para automóveis comuns. Normalmente, não se aumenta muito devido a possibilidade de autoignição, ou por "bater bielas", a qual impõe valores de compressão acima do limite superior da taxa de compressão.^[6] Durante o processo de compressão 1-2 a temperatura aumenta, assim um aumento da taxa de compressão aumenta a temperatura. Autoignição ocorre quando a temperatura da mistura combustível/ar se torna muito elevada antes de ser inflamada pela ignição. O curso de compressão é destinado para comprimir os produtos antes que a ignição inflame a mistura. Se a taxa de compressão é aumentada, a mistura pode se autoinflamar antes do curso de compressão ser finalizado, levando o motor a "bater biela". Isto pode danificar os componentes do motor e vai diminuir a potência de freio do motor.

Referências

Bibliografia |

• Desenvolvimento de um Range Extender baseado num motor BMW K75: transformação de ciclo Otto para ciclo Miller. Dissertação de mestrado. Pedro Joaquim Pereira dos Santos.Universidade de Minho - Escola de Engenharia.


• Sistema de Desenvolvimento para controle eletrônico dos motores de combustão interna Ciclo Otto. Dissertação de Mestrado.Carlos Eduardo Milhor. Escola de Engenharia de São Carlos - EESC - USP.


• Fundamentos de Física, volume 2 - 8 edição: gravitação, ondas e termodinâmica/ Halliday,Resnick, Jearl Walker: tradução e revisão técnica Ronaldo Sérgio de Biasi - Rio de Janeiro, LTC,2009

Este artigo sobre Termodinâmica é um esboço. Você pode ajudar a Wikipédia expandindo-o.