Yhyjyk

Este artigo ou secção contém fontes no fim do texto, mas que não são citadas no corpo do artigo, o que compromete a confiabilidade das informações. (desde julho de 2011) Por favor, melhore este artigo inserindo fontes no corpo do texto quando necessário.

Esta página precisa ser reciclada de acordo com o livro de estilo (desde julho de 2011). Sinta-se livre para editá-la para que esta possa atingir um nível de qualidade superior.

Um Pequeno Lema |

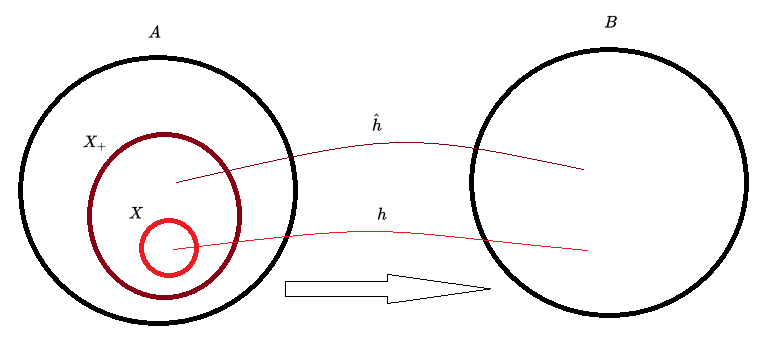
Seja A um conjunto não vazio, X um subconjunto de A, F um conjunto de funções em A, e X+displaystyle X_+ o fecho indutivo de X sob F.

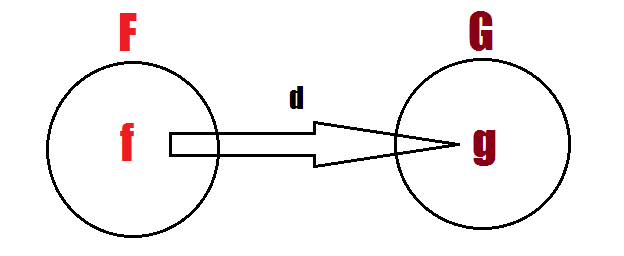
Seja B qualquer conjunto não vazio e seja G o conjunto de funçoes sobre o conjunto B, de forma que exista uma função d:F→Gdisplaystyle d:Fto G em G ,que associa com cada função f de aridade n em F a seguinte função d(f):Bn→Bdisplaystyle d(f):B^nto B em G(G não pode ser uma bijeção).

Partindo deste lema podemos construir o conceito de Extensão Homomórfica Unica.

O Teorema |

Se X+displaystyle X_+ é livremente gerado por X e F , para cada função h:X→Bdisplaystyle h:Xto B existe uma única função h^:X+→Bdisplaystyle hat h:X_+to B tal que:

 (1)∀x∈X,h^(x)=h(x)displaystyle forall xin X,hat h(x)=h(x);
 Para toda função f de aridade n > 0, para para todo x1,...,xn∈X+n,displaystyle x_1,...,x_nin X_+^n,

 (2)h^(f(x1,...,xn))=g(h^(x1),...,h^(xn)),ondeg=d(f)displaystyle hat h(f(x_1,...,x_n))=g(hat h(x_1),...,hat h(x_n)),onde,g=d(f)

Implicações |

As identidades vistas em (1) e (2) demonstram que h^displaystyle hat h é um homomorfismo, chamado especificamente de Extensão Homomórfica Única de hdisplaystyle h. Para provar o teorema, dois requisitos devem ser satisfeitos: provar que a extensão(h^displaystyle hat h) existe e é única (garantindo a ausência de bijeções).

Prova do Teorema da Extensão Homomórfica Unica |

Precisamos definir uma sequencia de funções hi:Xi→Bdisplaystyle h_i:X_ito B de forma indutiva , satisfazendo as condições (1) e (2) restritas a Xidisplaystyle X_i. Para isso definimos h0=hdisplaystyle h_0=h e dado hidisplaystyle h_i então hi+1displaystyle h_i+1 terá o seguinte grafo (lembre-se, estamos tratando um homomorfismo e portanto precisamos provar isso via grafos):

 (f(x1,...,xn),g(hi(x1),...,hi(xn)))∪grafo(hi)displaystyle (x_1,...,x_n)in X_i^n-X_i-1^n,fin Fcup grafo(h_i) com g=d(f)displaystyle g=d(f)

Primeiro devemos checar se o grafo realmente possui funcionalidade, já que X+displaystyle X_+ é livremente gerado, pelo pequeno lema temos que f(x1,...,xn)∈Xi+1−Xidisplaystyle f(x_1,...,x_n)in X_i+1-X_i quando (x1,...,xn)∈Xin−Xi−1n,(i≥0)displaystyle (x_1,...,x_n)in X_i^n-X_i-1^n,(igeq 0),então preciamos apenas determinar a funcionalidade apenas para a primeira parte da união. Tendo que os elementos de G são funções(novamente, como definido pelo lema), a unica possibilidade de ter (x,y)∈grafo(hi)displaystyle (x,y)in grafo(h_i) e (x,z)∈grafo(hi)displaystyle (x,z)in grafo(h_i) para algum x∈Xi+1−Xidisplaystyle xin X_i+1-X_i é ter x=f(x1,...,xm)=f′(y1,...,yn)displaystyle x=f(x_1,...,x_m)=f'(y_1,...,y_n) para algum (x1,...,xm)∈Xim−Xi−1m,(y1,...,yn)∈Xin−Xi−1ndisplaystyle (x_1,...,x_m)in X_i^m-X_i-1^m,(y_1,...,y_n)in X_i^n-X_i-1^n e para alguns construtores fdisplaystyle f e f′displaystyle f' em Fdisplaystyle F.

Já que f(X+m)displaystyle f(X_+^m) e f′(X+n)displaystyle f'(X_+^n) são disjuntos quando f≠f′,f(x1,...,xm)=f′(y1,...,Yn)displaystyle fneq f',f(x_1,...,x_m)=f'(y_1,...,Y_n)isto implica que f=f′displaystyle f=f' e m=ndisplaystyle m=n. Sendo todo f∈Fdisplaystyle fin F em X+ndisplaystyle X_+^n,nós temos que ter xj=yj,∀j,1≤j≤ndisplaystyle x_j=y_j,forall j,1leq jleq n.

Mas então temos y=z=g(x1,...xn)displaystyle y=z=g(x_1,...x_n) com g=d(f)displaystyle g=d(f), mostrando funcionalidade.

Antes de continuar precisamos utilizar um novo lema que determine regras para funções parciais, ele pode ser escrito como:

 (3)Seja (fn)n≥0displaystyle (f_n)_ngeq 0 uma sequencia parcial de funções fn:A→Bdisplaystyle f_n:Ato B tal que fn⊆fn+1,∀n≥0displaystyle f_nsubseteq f_n+1,forall ngeq 0. Então, g=(A,⋃grafo(fn),B)displaystyle g=(A,bigcup grafo(f_n),B) é uma função parcial. [1]

Usando (3), h^=⋃i≥0hidisplaystyle hat h=bigcup _igeq 0h_i é uma função parcial. Já que dom(h^)=⋃dom(hi)=⋃Xi=X+displaystyle dom(hat h)=bigcup dom(h_i)=bigcup X_i=X_+então h^displaystyle hat h é total em X+displaystyle X_+.

Indo além, é claro pela definição de hidisplaystyle h_i que h^displaystyle hat h satisfaz (1) e (2). Para provar a unicidade de h^displaystyle hat h, para qualquer outra função h′displaystyle h' que satifaça (1) e (2), basta usar uma indução simples que mostre que h^displaystyle hat h e h′displaystyle h' servem para Xi,∀i≥0displaystyle X_i,forall igeq 0, provando assim o Teorema da Extensão Homomórfica Unica.[2]

Exemplo de Caso Particular |

Podemos usar o teorema da extensão no calculo numérico de expressões sobre números inteiros. Primeiramente devemos definir o seguinte:

A=Σ∗displaystyle A=Sigma ^* onde Σ=Variaveis∪0,1,2,...9∪+,−,∗∪(,),onde∗=Variaveis∪0,...,9displaystyle Sigma =Variaveiscup 0,1,2,...9cup +,-,*cup (,),onde,*=Variaveiscup 0,...,9

Seja F=f−,f+,f∗displaystyle F=f-,f+,f*

f:Σ∗→Σw↦−w∗displaystyle f:Sigma ^*to Sigma _wmapsto -w^*

f:Σ∗xΣ∗→Σw1,w2↦w1+w2∗displaystyle f:Sigma ^*xSigma ^*to Sigma _w_1,w_2mapsto w_1+w_2^*

f:Σ∗xΣ∗→Σw1,w2↦w1∗w2∗displaystyle f:Sigma ^*xSigma ^*to Sigma _w_1,w_2mapsto w_1*w_2^*

Seja EXPRdisplaystyle EXPR o fecho indutivo de Xdisplaystyle X sob Fdisplaystyle F e seja
B=Z,G=Soma(−.−),Mult(−,−),Menos(−)displaystyle B=mathbb Z ,G=Soma(-.-),Mult(-,-),Menos(-)

Seja d:F→Gdisplaystyle d:Fto G

d(f−)=menosdisplaystyle d(f-)=menos

d(f+)=maisdisplaystyle d(f+)=mais

d(f∗)=multdisplaystyle d(f*)=mult

Então h^:X+→0,1displaystyle hat h:X_+to 0,1 será uma função que calcula recursivamente o valor-verdade de uma proposição, e de certa forma, será uma extensão de função h:X→0,1displaystyle h:Xto 0,1 que associa um valor verdade a cada proposição atômica,tal que:

(1)h^(ϕ)=h(ϕ)displaystyle hat h(phi )=h(phi )

(2)h^((¬ϕ))=NAO(h^(ψ))displaystyle hat h((neg phi ))=NAO(hat h(psi )) (Negação)

h^((ρ∧θ))=E(h^(ρ),h^(θ))displaystyle hat h((rho land theta ))=E(hat h(rho ),hat h(theta )) (Operação E)

h^((ρ∨θ))=OU(h^(ρ),h^(θ))displaystyle hat h((rho lor theta ))=OU(hat h(rho ),hat h(theta )) (Operação OU)

h^((ρ→θ))=SEENTAO(h^(ρ),h^(θ))displaystyle hat h((rho to theta ))=SE,ENTAO(hat h(rho ),hat h(theta )) (Operação Se-Então)

Referências |

• Gallier, Jean H, 2003, Logic For Computer Science: Foundations of Automatic Theorem Proving, pag 35


• Gallier, Jean H, 2003, Logic For Computer Science: Foundations of Automatic Theorem Proving, pag 45-46

Este artigo sobre matemática é um esboço. Você pode ajudar a Wikipédia expandindo-o. v d e

• Portal da matemática